If everything is composed of waves, then we also have to explain what charge is in this model, and how electromagnetism arises from it.
The wave needs to be such that a) there are only two types of charges (positive and negative), and it has to be compatible with spin 1/2, meaning, the wave motion of spin, which indices a magnetic field, has to be consistent with the model of the charge wave.
The solution is a circular, oscillating “wobbling” motion of the elastic solid, so that it is spherically symmetrical, and so that it does not “break” the solid anywhere. One direction is plus charge, the other direction is negative charge:
The simulation below best illustrates this – it might take a while to “see” it:
https://jsfiddle.net/Chenopdodium/hnbzt08d

The important point is: if you look at points on the surface of the sphere (note, the sphere is only a visual aid, it has otherwise no meaning!), the points (in the elastic solid) move in the same direction – on all sides.
It is easier to when we highlight multiple points in the elastic solid and show its movement:

When we “zoom out”, add a second charge to the scene and hide the cirles, and just show the arrows that indicate the direction of the wobble, it gets clearer:
https://jsfiddle.net/Chenopdodium/k7r320jx
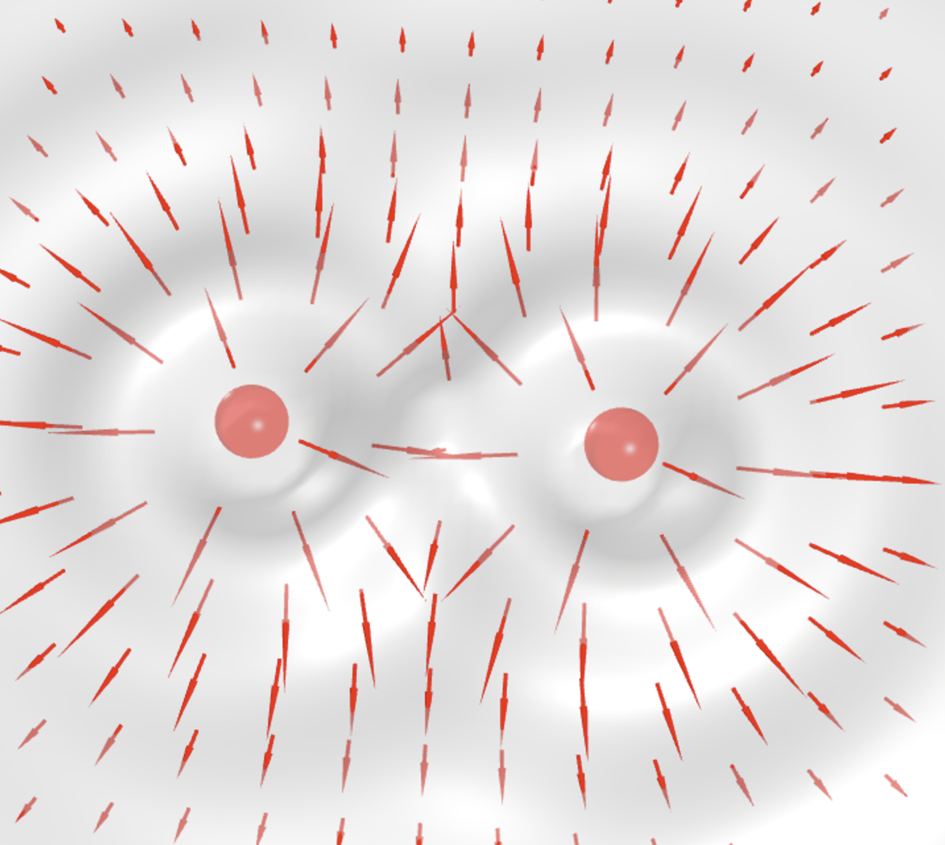
Here are two equal charges:
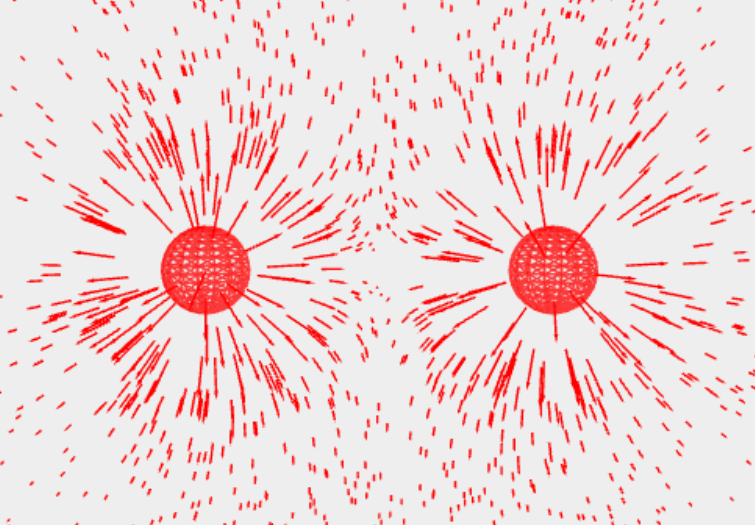
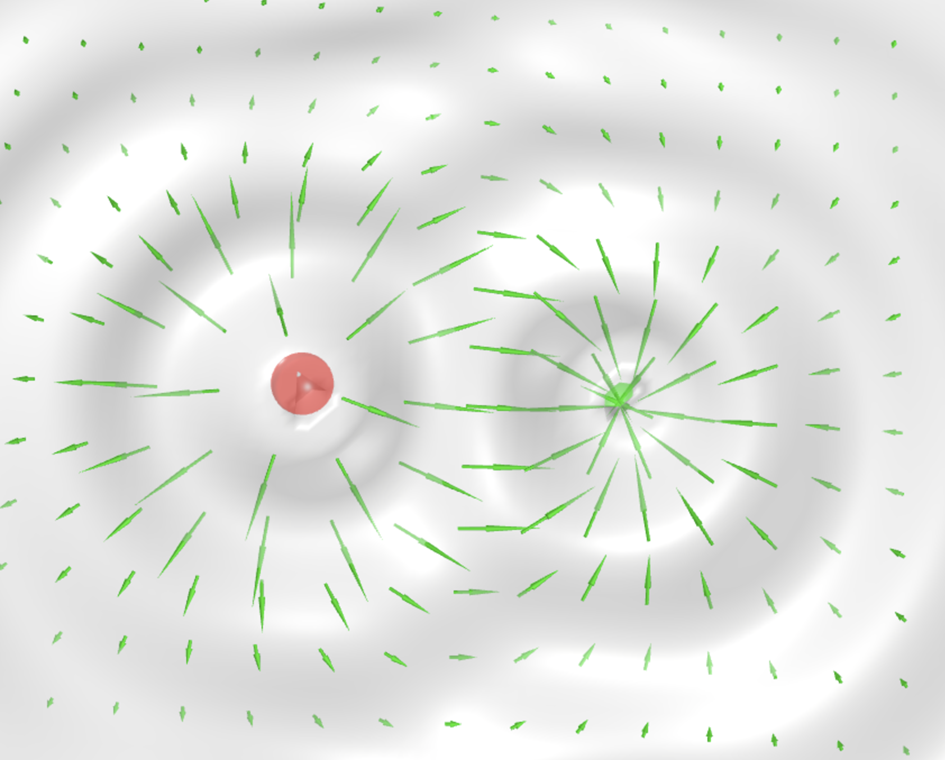
Opposite charges:
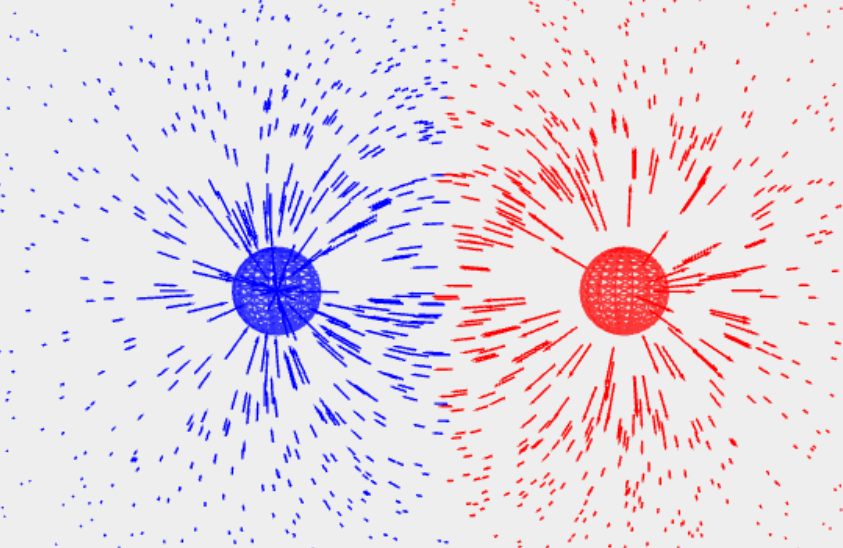
Note that the calculation is all based on the wave model, on the very simple wobbling motion!
Now we can go further of course, and ask, what happens as we accelerate a charge:
https://jsfiddle.net/Chenopdodium/kv0mx41n
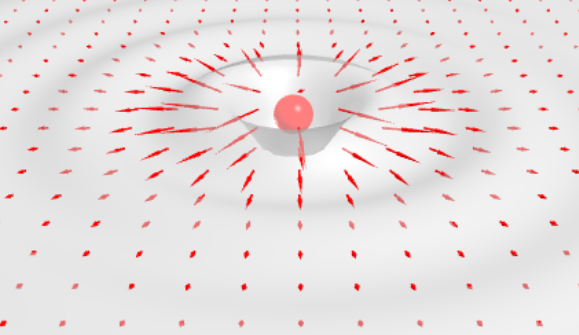
Note that again, the sphere is only a visual aid. It has *no meaning* other than indicating the center of the charge.
The plane shows the amplitude of the charge in the y direction to see the resulting wave motion.
Let’s add the magetic field as well, which is locally computed based on the curl of the electric field:
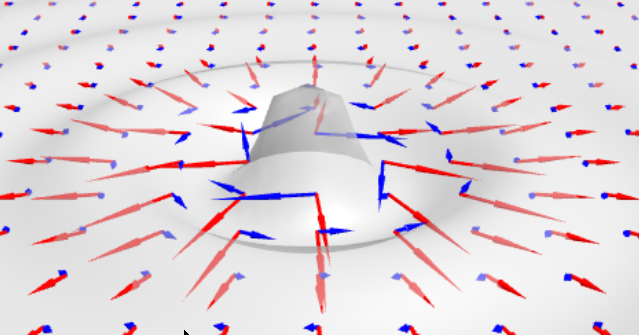
We can zoom in and only show a section to see it better (select only show y component, select show slice):

You can also add multiple charges, equal or opposite, and change the distance:
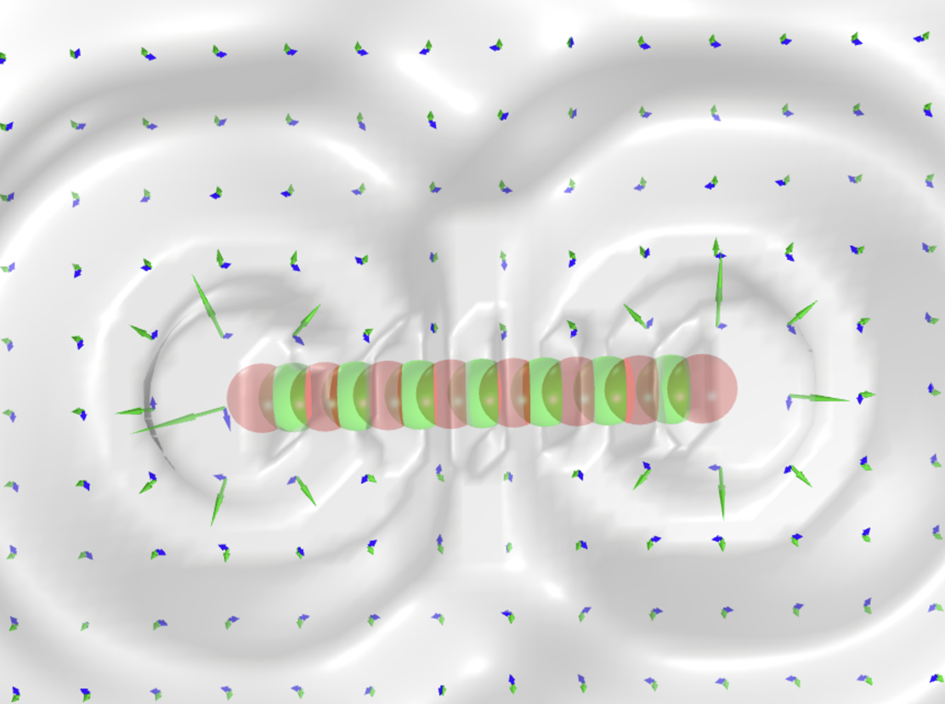
You can see that when we have a whole series of charges in a row, you get plane waves:

We can also alternate them:
Displacement Field
To mathematically describe the wobbling motion of charge within the framework of the Cauchy model of elastic solids, we’ll need to formulate the problem using the principles of continuum mechanics and wave propagation in elastic media.
Spherical Coordinates: Since the motion is radially symmetrical but tangential (perpendicular to the radius), it’s natural to use spherical coordinates
$$
\mathbf{u}(\mathbf{r}, t) = A(r) \sin(\omega t) \hat{\phi}
$$
- \( A(r) \): Amplitude function depending on radial distance $ r $
- \( \omega \): Angular frequency of the wobble.
- \( \hat{\phi} \): Unit vector in the azimuthal direction.