Spin 1/2
This album Album has a few videos on this topic (but no comments)
Here is a JavaScript version in JSFiddle:
Spin 1/2 has a few interesting properties: the configuration repeats after 2 “rotations” of the part in the center.
First the famous “Dirac belt trick” is shown:
This spinor never breaks the grid – the lines are always continuously connected to the “outside”, and no knots are created. Below ist the same spinor as above, just visualized differently, with a grid instead of a belt.
(A sphere is added on the right only for visualization purposes – it has nothing to do with spin itself.)
Imagine that we zoom out a bit and hide he “inside” with a sphere ( please note that the sphere is only added for pure visualization purposes and has no meaning.). In the video below, we start zoomed out (the sphere is large). So the spin wave looks like a small wobble, like a precession. Later in the video we zoom in a bit (imagine the sphere getting smaller), and the wobble gets more extreme. The full spin 1/2 is when the “sphere” is turned all the way upside down, 180 degrees. It the appears to to rotate in a circle. Note that it never “breaks” the grid!
Also note that it takes two full rotations of the sphere to get the spatial configuration back to the start:
Let’s look at spin with 2 “particles” – note that the second one appears to rotate in the other direction. This is necessary in order to keep the grid intact. If we move them closer, and if we align the spin, it does not work, as shown briefly roughly from 0:23s – 0:39s (before and after the spins are opposite).
Here are some pictures that show the strain on the grid. You can see that when spins are opposite, the strain is less than when the spins point in the same direction:
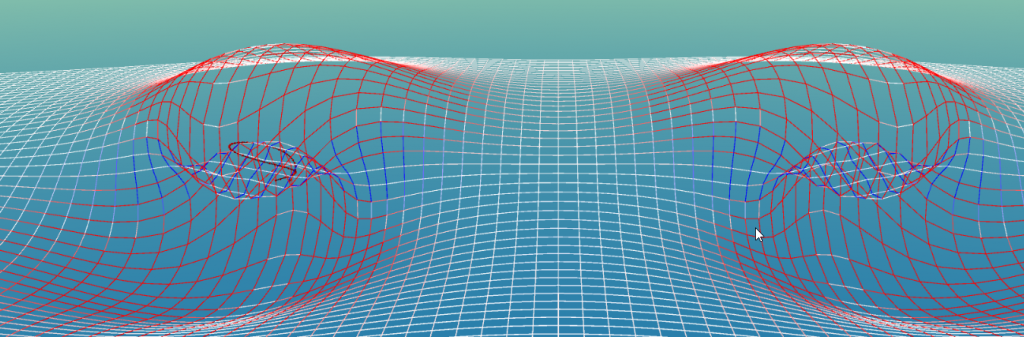
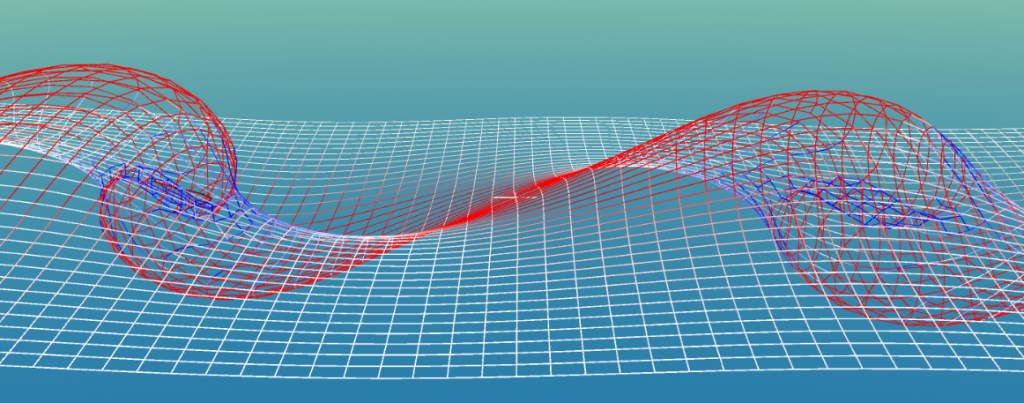
More complex spinors are of course possible:
A bunch of additional videos that all show different views of the exact same thing.
Below is a view where I show how some points round the electron wobble around.
Here I show how a few points wobble around (red circles). The red spikes show the centers of that wobble twist. Note that these are not rotations, but wobble that require 720 degrees to return to the start. It is just a different view of the exact same spin 1/2 visualiation as the others.